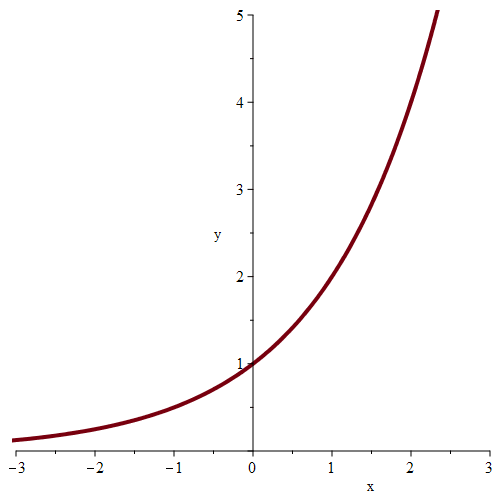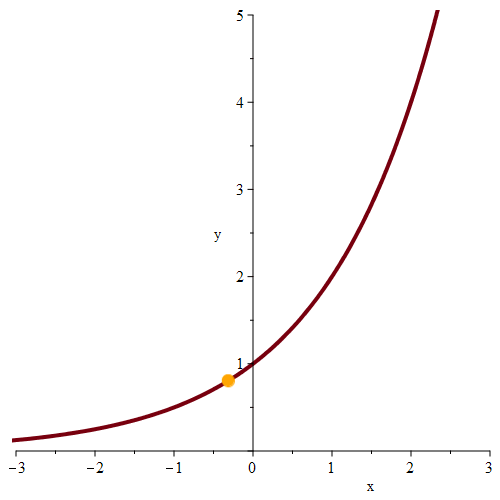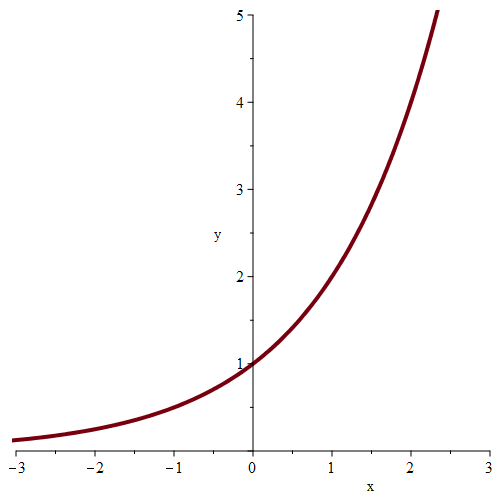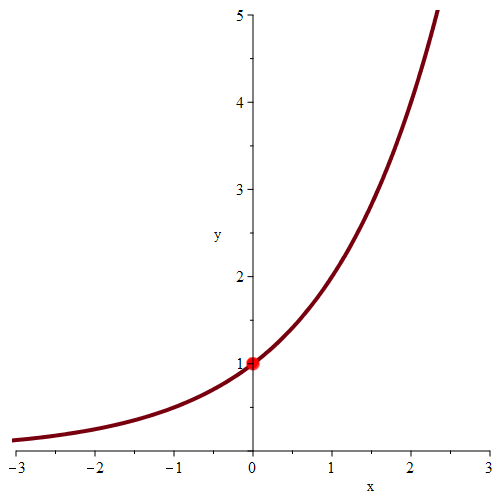1 收敛与发散
|
收敛 |
发散 |
| 图像表示 |
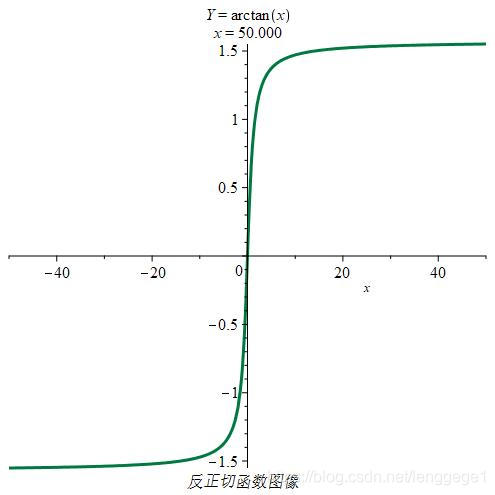 |
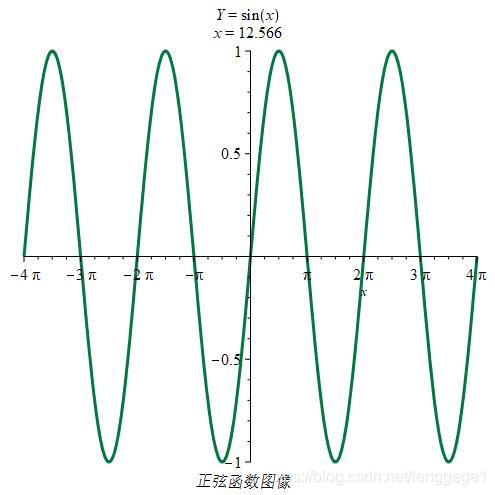 |
| 意义 |
趋近于某个固定值,如图函数 y=arctanx,x→∞,y≈2π |
不存在一个常数a,使得x趋近无穷大时等于该常数,
如图y=sinx,x→∞,无法确定y趋近于何值 |
| 表达式 |
x→∞limf(x)=a |
x→∞limf(x)=a |
| 用途 |
函数有极限 |
函数无极限 |
2 极限
如图所示,当x从两侧趋近于0时,y趋近于1。极限的思想即为无限逼近思想。
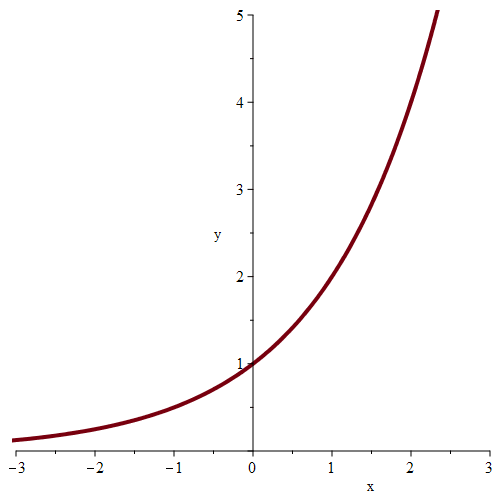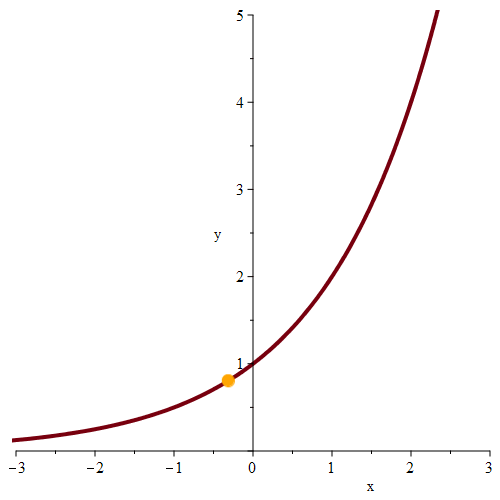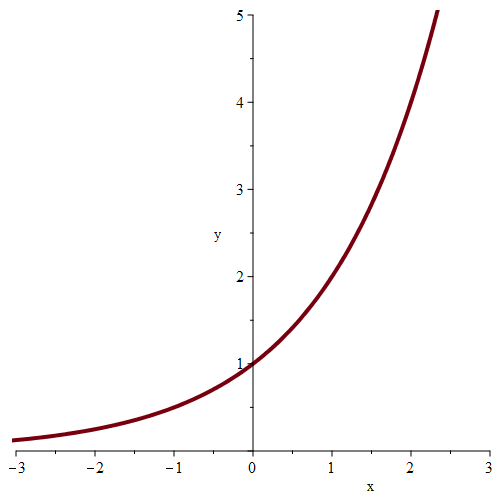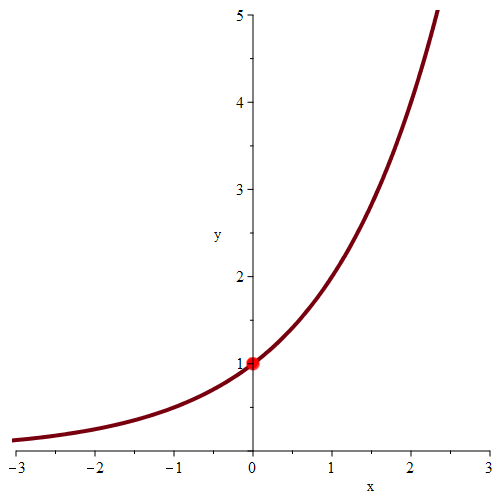
2.1 极限与单侧极限
|
极限 |
左极限 |
右极限 |
| x→x0 |
x→x0limf(x)=A |
x→x0−limf(x)=A |
x→x0+limf(x)=A |
| x→∞ |
x→∞limf(x)=A |
x→−∞limf(x)=A |
x→+∞limf(x)=A |
2.2 极限关系
|
关系 |
| x→x0 |
x→x0limf(x)=A⟺x→x0−limf(x)=x→x0+limf(x)=A |
| x→∞ |
x→∞limf(x)=A⟺x→−∞limf(x)=x→+∞limf(x)=A |
2.3 函数极限性质
-
唯一性:若数列的极限存在,则极限值是唯一的。
-
有界性:如果一个函数(数列)收敛(有极限),那么这个函数(数列)一定有界。但是,如果一个数列有界,这个数列未必收敛。例如数列 :“1,-1,1,-1,……,(-1)n+1”
-
保号性:若x→∞limf(x)=A>0 (或<0),则对任何m∈(0,a)(a<0时则是m∈(a,0)),存在N>0,使n>N时,有xn>m(相应的xn<m)。
-
保不等式性:设数列{xn} 与{yn}均收敛。若存在正数N,使得当n>N时有xn≥yn,则
x→+∞limxn≥x→+∞limyn(若条件换为xn>yn,结论不变)。
3 极限的四则运算
3.1 函数的极限运算法则
设 xlimf(x)=A,xlimg(x)=A
| 运算 |
运算法则 |
| 和差 |
xlimf(x)±g(x)=A±B |
| 乘 |
xlimf(x)g(x)=AB |
| 商 |
xlimg(x)f(x)=BA(B=0) |
3.2 复合函数的极限运算法则
设f(x)=b0xm+b1xm−1+⋯+bma0xn+a1xn−1+⋯+am,则有:
x→∞limf(x)=⎩⎪⎨⎪⎧∞b0a00n>mn=mn<m
此处看上去很复杂,但却非常好记,该方法也叫抓大头法求极限,看个例子放松一下吧!
-
已知函数 f(x)=x3+x5x4+x2+5,求极限x→∞limf(x).
解:x→∞limf(x)=x→∞limx3+x5x4+x2+5=x→∞lim5x=∞
-
已知函数 f(x)=x3+x5x3+x2+5,求极限x→∞limf(x).
解:x→∞limf(x)=x→∞limx3+x5x3+x2+5=x→∞lim5=5
-
已知函数 f(x)=x4+x5x3+x2+5,求极限x→∞limf(x).
解:x→∞limf(x)=x→∞limx4+x5x3+x2+5=x→∞limx1=0