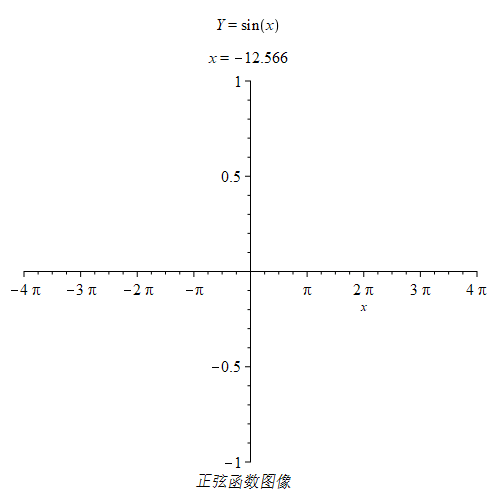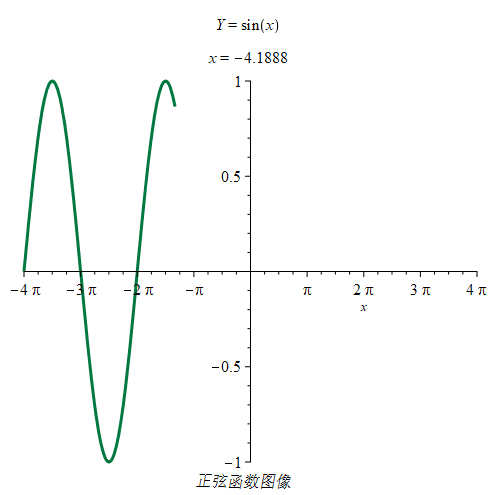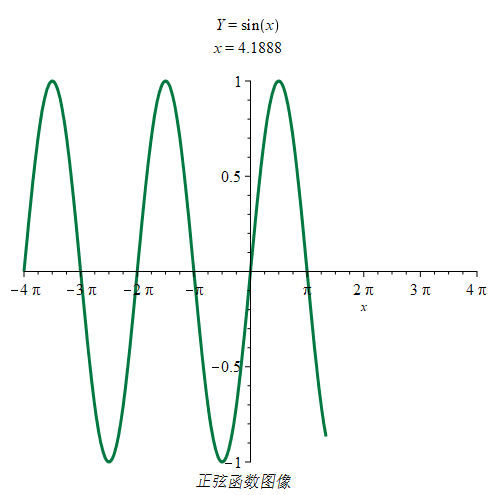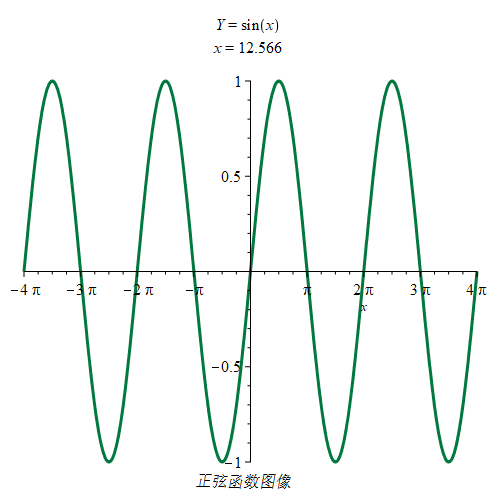G-No.1 初探函数性质与图像

• • 1 函数性质
    • 1.1 有界性
    • 1.2 单调性
    • 1.3 奇偶性
    • 1.4 周期性
  • 2 基本初等函数图像
    • 2.1 三角函数曲线图像
    • 2.2 幂函数
    • 2.3 指数函数与对数函数
  • 3. 复合函数
  • 4 初等函数

1 函数性质

1.1 有界性

  在定义域内的某个区间 $y$ 是等于或趋近于某个常数值 $c$，其数学语言表达为：$|y| \leq c$

• 举栗子

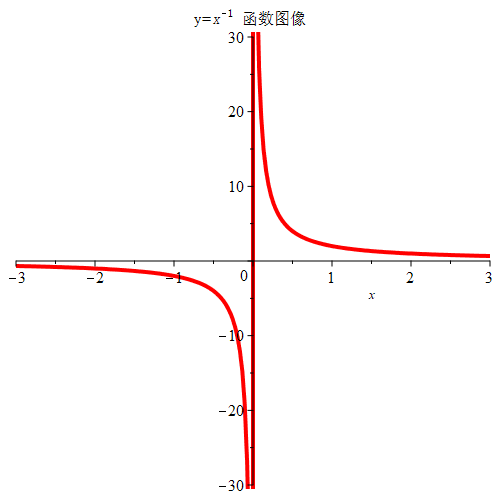
  如图是函数$y=x^{-1}=\frac{1}{x}$ 的函数图像，该函数在区间（0,1）上是无界的，在（1，+$\infty$] 上是有界的。

1.2 单调性

  单调性具有全局单调性与局部单调性，在求解单调性时请注意 $x$ 的取值范围。

• 举栗子

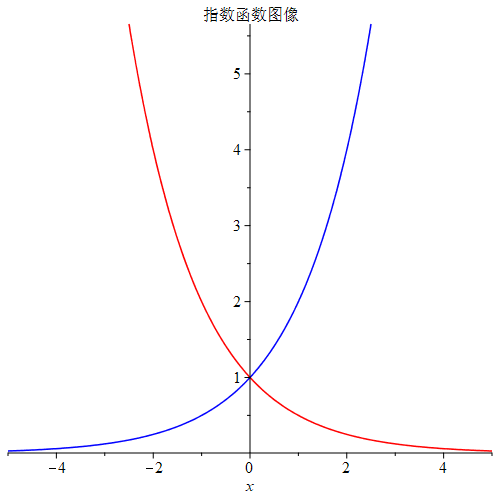
  如下图所示是指数函数 $y=a^x$。当 $0<a<1$ 时，$x \in [-\infty,\infty]$，单调递减；当 $a>1$ 时， $x \in [-\infty,\infty]$，单调递增。

1.3 奇偶性

• 举栗子

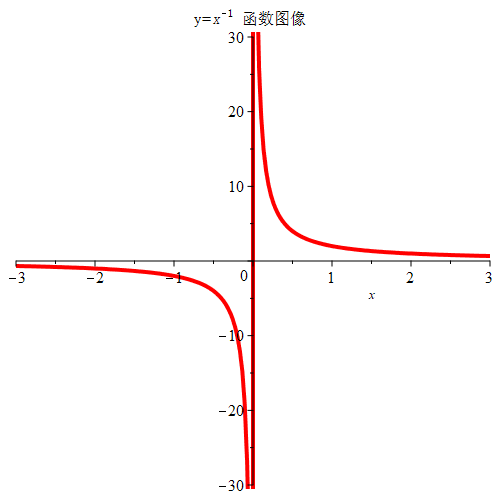
  如图是反比例函数图像。函数图像关于原点对称，也满足数学表达式 $f(x)=-f(-x)$，因此，函数 $y=\frac{1}{x}$ 是奇函数。

1.4 周期性

  若存在一非零常数$T$，对于定义域内的任意x，使$f(x)=f(x+T)$恒成立，则$f(x)$叫做周期函数，$T$ 叫做这个函数的一个周期。

• 举栗子

  如图是正弦函数图像，其周期为：$T=2\pi$，周期通常指最小周期。

2 基本初等函数图像

2.1 三角函数曲线图像

函数	函数图像	性质
正弦函数		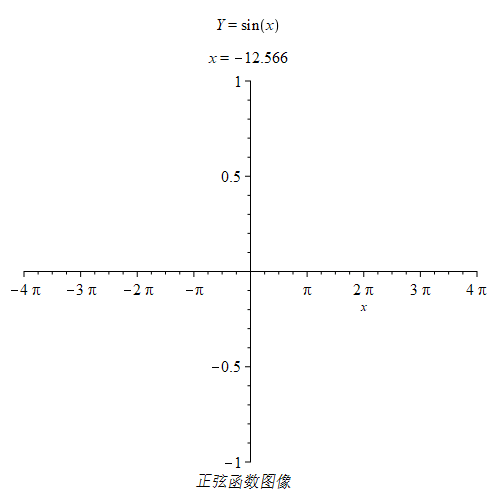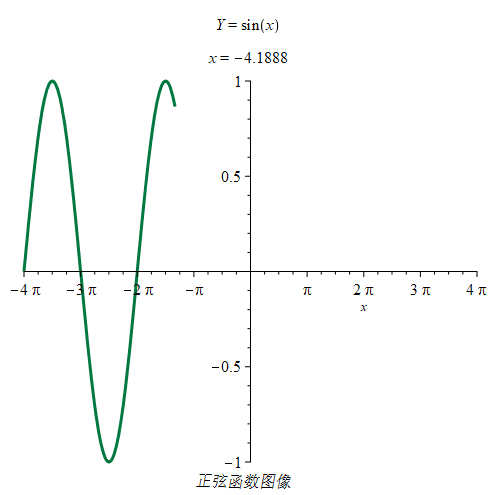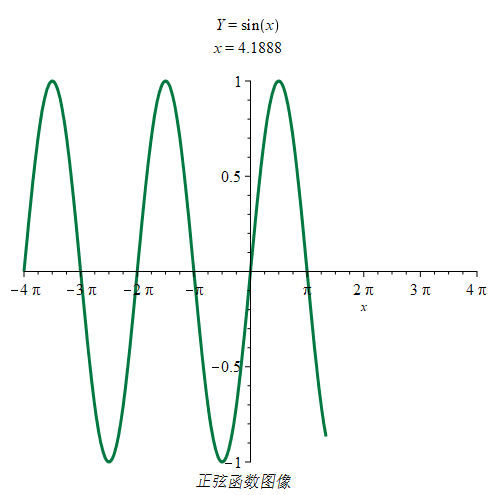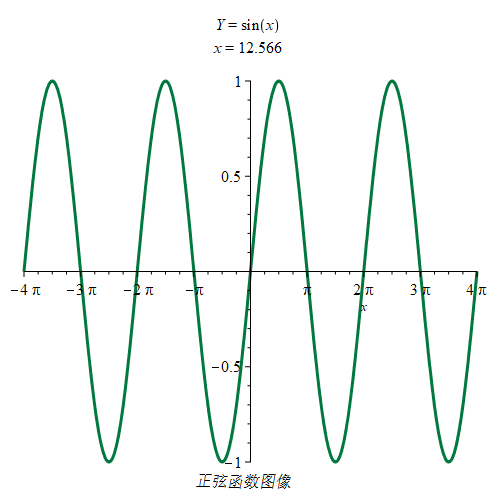奇偶性：奇函数 定义域：$x \in R$ 值域：$y \in [-1,1]$
余弦函数		奇偶性：偶函数 定义域：$x \in R$ 值域：$y \in [-1,1]$
正切函数		奇偶性：奇函数 定义域：$x \in [-\frac{\pi}{2},\frac{\pi}{2}]$ 值域：$y \in R$
三角函数曲线		对比三者的走势
反正弦函数		奇偶性：奇函数 定义域：$x \in [-1,1]$ 值域：$y \in [-\frac{\pi}{2},\frac{\pi}{2}]$
反余弦函数		奇偶性：非奇非偶函数 定义域：$x \in [-1,1]$ 值域：$y \in [0,\pi]$
反正切函数		奇偶性：奇函数 定义域：$x \in R$ 值域：$y \in [-\frac{\pi}{2},\frac{\pi}{2}]$
反三角函数曲线		对比三者的走势
双曲函数		1.注意双曲函数$\not =$双曲线 2.注意双曲函数与三角函数无关 3.例：$y=sinhx=\frac{e^x-e^{-x}}{2}$

2.2 幂函数

  幂函数的表达式为：$y=x^a$，a的取值不同，其曲线形状、定义域与值域也各不相同。

2.3 指数函数与对数函数

指数函数是对数函数的反函数

	指数函数 $y=a^x$	对数函数 $y=log_a^x$
$0<a<1$
$a>1$
整合对比图

3. 复合函数

• 定义：由两个（或两个以上）的基本初等函数复合而成的函数

• 举栗子

  如图所示是两个简单函数【$f(x)=2x^2+1、g(x)=\frac{1}{x}$】及其由这两个简单函数复合得到的复合函数【$f(g(x))=2(\frac{1}{x})^2+1、g(f(x))=\frac{1}{2x^2+1}$】的图像。

  注意：有些函数是不能进行复合的，如：$y=arcsinu,u=x^2+3$，因为前者的定义域与后者的值域的交集为空集，无意义！

4 初等函数

  初等函数是由幂函数、指数函数、对数函数、三角函数、反三角函数与常数经过有限次的有理运算（加、减、乘、除、有理数次乘方、有理数次开方及有限次函数复合所产生，并且能用一个解析式表示的函数。

  分段函数一般不是初等函数!